Necharakteristická hodnota

Ve středoevropském regionu se začaly používat první normy pro navrhováních stavební konstrukcí v třicátých letech minulého století. Přibližně od osmdesátých let předminulého století byly vydávány různé stavební předpisy, převážně jako Stavební řády různých měst. Spolehlivost konstrukce byla dříve zajištěna většinou na základě zkušeností stavitele stavby, v novější době dokladována výpočtem, kterým se prokazuje splnění podmínek spolehlivosti.
Spolehlivost je obecně definovaná jako vlastnost věci sloužit účelu, pro který byla zhotovena. Takže spolehlivost nosné konstrukce znamená, že konstrukce se nesmí zřítit, nesmí se deformovat tak, aby byla obtížně použitelná, při požáru musí umožnit obyvatelům opustit objekt apod. Skutečné namáhání konstrukce, vlastnosti materiálů, geometrické tvary prvků, vznik porušení atd. jsou jevy tak složité, že jejich přesný matematický popis je nemožný. V každém výpočtu je třeba problém idealizovat zavedením souboru předpokladů tak, aby byl výpočet proveditelný. Idealizovaný stav, který vznikl zavedením souboru předpokladů do výpočtu, se nazývá výpočetní model. Tento model by měl obsahovat všechny podstatné prvky, které jsou z hlediska posouzení spolehlivosti konstrukce významně a má zanedbat prvky nepodstatné. Výpočetní model hraje důležitou úlohu při návrhu konstrukce, popř. konstrukčního prvku.
Způsob zahrnutí nejistot a zajištění spolehlivosti konstrukcí při navrhování se vyvíjel v úzké závislosti na dostupných experimentálních i teoretických poznatcích v oblasti stavební mechaniky, teoretické pružnosti a matematické statistiky. Vývoj různých metod navrhování stavebních konstrukcí se ve dvacátém století postupně ustálil na třech všeobecně používaných metodách, které se v různých modifikacích uplatňují v normách pro navrhování konstrukcí dodnes.

Metoda dovolených namáhání

První celosvětově rozšířenou metodou navrhování stavebních konstrukcí byla metoda dovolených namáhání. Vychází z podmínky, že namáhání materiálu σ _dov je menší než namáhání materiálu při porušení σ _krit dělené součinitelem k.

σ _dov < σ _krit /k (1)

Součinitel k je zde stanoven s ohledem na nejistoty při stanovení účinku zatížení i odolnosti materiálu, a má tedy s dostatečnou zárukou zajistit spolehlivost celé konstrukce. Hlavní nedostatky metody dovolených namáhání se objevují při ověřování spolehlivosti (v elastickém oboru): nemožnost individuálního přihlédnutí k nejistotám jednotlivých základních veličin a k nejistotám výpočtových modelů pro stanovení účinku zatížení i odolnosti konstrukce. Pravděpodobnost poruchy lze u této metody explicitně ovlivnit pouze jedinou veličinou, součinitelem k.
Vlastnosti materiálů ovlivňující odolnost nosné konstrukce se v metodě dovolených namáhání obvykle vyjadřovaly průměrnými hodnotami získanými při zkouškách pevnosti. Vyjádřeno přesněji aritmetickým průměrem z výsledků zkoušek pevnosti materiálu. Počet zkoušek na určitý objem materiálu byl předepsán v normách nebo jiných technických předpisech zcela nahodile na základě dohody zpracovatelů normy. Z hlediska stavebního inženýra jednoduše pochopitelná záležitost: provedu zkoušky, zjistím pevnost materiálu, a když tuto pevnost vydělím jakýmsi součinitelem, obdržím dovolené namáhání. Pokud výpočtem prokáži, že nikde není toto dovolené namáhání překročeno, je konstrukce spolehlivá.
Koeficient, kterým se dělila průměrná hodnota pevnosti materiálu, se obvykle nazýval ?koeficient bezpečnosti? a například v Technickém průvodci pro inženýry a stavitele z roku 1896 se pohyboval v rozmezí od hodnoty 3 pro kujné železo do hodnoty 30 pro kamenné mosty.Tímto koeficientem inženýr vyjadřoval intuitivně množství nejasností a neznámých skutečností, které ovlivňují bezpečnost konstrukce. Proto známý odborník v oblasti teoretické mechaniky Štěpán P. Timošenko tento koeficient někdy nazýval ?koeficientem neznalostí? nebo ?koeficientem naší ignorance?.

Metoda stupně bezpečnosti

Druhou všeobecně rozšířenou metodou navrhování stavebních konstrukcí byla metoda stupně bezpečnosti. Tato metoda rovněž vycházela z průměrných nebo přibližně průměrných pevností materiálů. Z těchto hodnot se vypočítala únosnost průřezu a takto určená hodnota únosnosti průřezu musela být o určitý násobek větší, než bylo namáhání od zatížení.
Metoda vychází z podmínky:

X _odol /X _krit, > s0 (2)

podle které má být vypočítaný stupeň bezpečnosti ?s? větší než jeho předepsaná hodnota ?s_o?. Jde o metodu, která se snaží především o dokonalejší vystižení chování prvku a jejich průřezů vyjádřené souhrnnými veličinami odolnosti průřezu X _odol a účinku zatížení X _krit. Stejně jako u metody dovolených namáhání zůstává hlavním nedostatkem nemožnost přihlédnout k nejistotám jednotlivých základních veličin a teoretických modelů. Pravděpodobnost poruchy lze u této metody explicitně ovlivnit opět pouze jedinou veličinou, stupněm bezpečnosti ?s?.

Metoda mezních stavů
Přibližně v polovině minulého století je zaváděna do praxe nová metoda navrhování stavebních konstrukcí, kterou se spolehlivost konstrukcí ověřuje metodou dílčích součinitelů spolehlivosti, nazývaná jako metoda mezních stavů. Při vlastním navrhování touto metodou jsou vstupními veličinami výpočetního modelu charakteristické (popř. reprezentativní) hodnoty zatížení a materiálu a dílčí součinitele spolehlivosti. Metoda odstraňuje některé nedostatky dřívějších metod, tj. umožňuje diferencovat váhu jednotlivých účinků zatížení, které působí na spolehlivost konstrukce a přihlíží k variabilitě vlastností stavebních materiálů. Tato metoda se také nazývá metodou parciálních součinitelů spolehlivosti a používá se v návrhových normách v současné době.

Stručná statistika pro nestatistiky
K variabilitě materiálových vlastností se v metodě parciálních součinitelů spolehlivosti přihlíží tím, že při hodnocení výsledků zkoušek se uvažuje nejen průměrná hodnota, ale také rozptyl výsledků kolem této průměrné hodnoty. Tímto krokem vstoupila do hry statistika, a tím se principy navrhování konstrukcí staly pro část technické veřejnosti krajně podezřelé, pro fundamentalisty v oboru až zločinné. Image statistiky je v široké veřejnosti velmi špatná, protože pod názvem statistika se velice často setkáváme se snahou přesvědčit veřejnost o něčem, co vůbec není pravda. Využívá se při tom záměrně povědomí většiny lidí, že co je vyjádřeno čísly, je správné, a čím více desetinných míst, tím je tvrzení důvěryhodnější. Toto je velmi dobře známo pracovníkům PR, reklamním agenturám i politikům. Vždy připomínají rozsáhlé statistické testy, které mají spotřebitele přesvědčit, že ?tento prací prášek? je výrazně lepší než ?prášek obvyklý?, nebo tato ?bílá je bělejší?. Výsledky těchto testů nejsou pro spotřebitele nikdy dostupné.
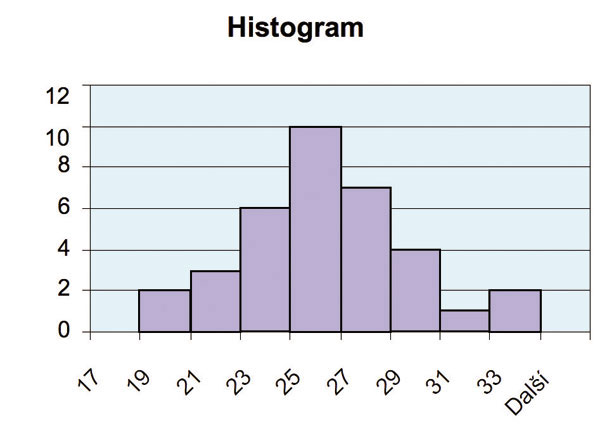
Při návrhu stavební nosné konstrukce pracuje stavební inženýr s reálnou hmotou a reálnými jevy, které mají téměř vždy náhodný charakter. Pevnost i jiné vlastnosti stavebních materiálů jsou charakterizovány nejen střední hodnotou, ale také rozptylem hodnot pevnosti kolem této střední hodnoty. Každý pracovník stavební laboratoře ví, že například výsledky zkoušek pevnosti určitého materiálu jsou rozdílné a že může, pokud má dost výsledků, sestavit diagram jako je na obr. 1. Jedná se o histogram četností, kde na vodorovné ose jsou hodnoty, v tomto případě hodnoty pevnosti betonu, a na svislé ose četnosti, tj. počet výsledků, které padnou do určitého intervalu na ose pevnosti. Charakteristická hodnota pevnosti je definována tak, že nižší pevnost než charakteristická hodnota se může vyskytovat pouze v 5 % případů zkoumaného souboru, tj. výsledků zkoušek. Velmi zjednodušeně je potřeba z barevné plochy oddělit část o velikosti 5 % a pevnost v daném místě je pevnost ?charakteristická?. Protože máme v daném případě 35 výsledků, jsou přibližně dva výsledky 5 % všech výsledků. Prvý obdélníček v histogramu představuje dva výsledky takže charakteristická pevnost bude přibližně 21,0 MPa, zatímco průměrná hodnota bude kolem 26,0 Mpa. Histogram tedy dává i neodborníkovi v dané problematice poměrně názorný obrázek, jaký je rozdíl mezi charakteristickou a průměrnou pevností. Všechny stavební materiály mají obdobný tvar histogramu četností jako je na obrázku 1. Nejvíce výsledků je kolem průměrné hodnoty a na obě strany výsledky postupně ubývají. Matematická statistika nahrazuje tento nepravidelný histogram analytickou funkcí, a tím umožní matematické zpracování i takových náhodných jevů, jako jsou výsledky zkoušek. Tato analytická funkce se nazývá rozdělení četností. Pro pevnost stavebních materiálů je nejběžnějším typem rozdělení, tzv. Normální rozdělení. Tvar tohoto rozdělení je na obr. 2. Toto rozdělení je závislé pouze na dvou veličinách tj. průměru a rozptylu, a proto se s ním dobře pracuje.
Statistika zavádí důležité pojmy ?základní soubor? a ?náhodný výběr?, které je třeba ve zkušebnictví důsledně rozlišovat. V případě zkoušek materiálu tvoří základní soubor všechny možné výsledky zkoušek, které bychom mohli při zkoušení určitého druhu materiálu obdržet. Náhodný výběr je soubor výsledků zkoušek, které jsme skutečně provedli. Na základě provedeného výběru, tj. často pouze několika zkoušek, odhadujeme vlastnosti základního souboru například jeho střední hodnotu nebo rozptyl. Tyto hodnoty můžeme pouze odhadnout, protože odebereme-li ze Základního souboru jiné prvky dostaneme jiné výsledky zkoušek, a tím jiný výběrový průměr a jiný výběrový rozptyl. Statistika však umí s předem určenou pravděpodobností určit interval, v němž bude hledaný parametr základního souboru. Čím je počet zkoušek větší, tím jsou uvedené intervaly užší.
Problém stanovení charakteristické pevnosti materiálu je v tom, že je třeba na základě pouze několika zkoušek, tj. náhodného výběru, určit kvantil 5 % základního souboru. V praxi to znamená rozdělit plochu, kterou určuje křivka rozdělení základního souboru a osa X na dvě části tak, aby jedna část byla 5 % a druhá 95 % celé plochy. Je zřejmé, že obdobně jako u průměru nebo rozptylu budeme moci s určitou pravděpodobností pouze odhadnout interval, ve kterém se charakteristická pevnost bude nacházet.

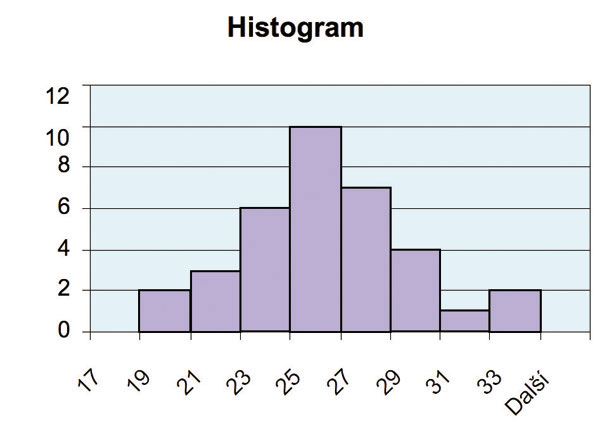
Obr. 1. Histogram četnosti

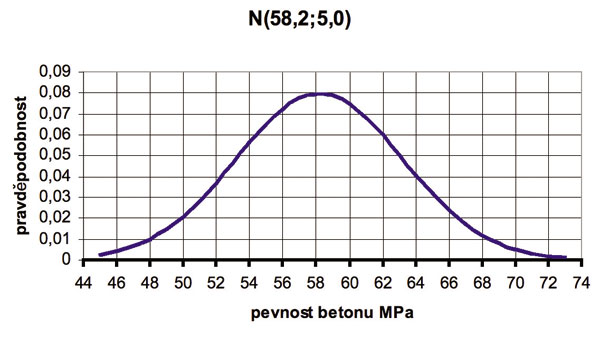
¤ Obr. 2. Normalni rozděleni

Charakteristická pevnost a stavební normy
Pojem charakteristická pevnost se v českých normách objevil poprvé v roce 1970. V té době byla zavedena nová norma ČSN 73 2400 Provádění a kontrola betonových konstrukcí místo dříve platné ČSN 73 2003 Stavební kontrola betonářských prací. Nová norma ponechávala původní hodnocení betonu na základě průměru získaného z výsledků zkoušek tří krychlí a hodnocení podle charakteristické pevnosti omezila na případy, kdy výsledky zkoušek betonu byly hodnoceny statisticky. V roce 1987 byla také vydána nová ČSN 73 2404 Statistická kontrola a posuzování jakosti betonu. Problematika hodnocení jakosti materiálu je dobře vidět, podíváme-li se zpětně na ustanovení v dříve platných normách. Téměř každá norma, často i novela, měla jiná kritéria pro hodnocení pevnosti materiálu. Pevnost v tlaku nebo v tahu byla přitom téměř vždy rozhodující pro spolehlivost konstrukce.
Statistické metody nenašly pochopení u technické veřejnosti. Jako důvod odporu ke statistickým metodám se ze začátku uváděla jejich pracnost. Příchodem kalkulaček a počítačů důvod pracnosti výpočtů pominul a bylo nutné najít důvod jiný. Důvody se našly a hned několik. Od zcela primitivních tvrzení jako ?statistické metody nelze použít, protože statistika lže? nebo ?statistické metody jsou drahé? až po zcela dokonalý způsob převzatý pravděpodobně z praxe reklamních agentur. Neodmítat statistické metody, naopak tvrdit, že statistické metody jsou použité, ale ve skutečnosti je vůbec nepoužít.
Charakteristická pevnost je v normách definována různě a často jsou tímto pojmem označovány různé veličiny. V jednom případě je tímto pojmem označován výše uvedený kvantil 5 % základního souboru nebo jeho odhad. Jedná se o proměnnou hodnotu, závislou na hodnoceném materiálu. V druhém případě se pojmem charakterická hodnota rozumí konstantní hodnota charakterizující druh materiálu. V Eurokódu 1992-1-1 je pro beton označený C20/25 uvedena charakteristická hodnota válcové pevnosti f_ck = 20 MPa, tj. konstantní hodnota. ČSN EN 206-1 Beton - Část 1: Specifikace, vlastnosti, výroba a shoda, deklaruje v čl. 3.1.32 charakteristickou pevnost jako hodnotu pevnosti, pro kterou lze očekávat nižší hodnoty nejvýše u 5 % základního souboru všech možných výsledků zkoušek pevnosti hodnoceného objemu betonu. V tomto případě je charakteristická hodnota pevnosti proměnná a závislá na zkoušeném betonu. Bylo by proto vhodné tyto veličiny odlišit a v případě, že se jedná o proměnou hodnotu, místo označení f_ck použít označení f_0,05.
Vycházíme-li ze zkoušek materiálu a máme k dispozici dostatečně velké množství zkoušek k tomu, abychom mohli s vysokou pravděpodobností stanovit parametry základního souboru, pak kvantil 5 % tohoto základního souboru je charakteristická hodnota pevnosti hodnoceného materiálu. Tyto vztahy jsou uvedeny na obr. 3. V něm je to hodnota 50,0 MPa. Abychom mohli předpokládat, že známe parametry základního souboru, musel by být počet zkoušek ovšem vysoký, tj. min. 200 až 300 zkoušek. Tento počet nepřichází v praxi v úvahu. Při reálně možném počtu zkoušek, tj. tři až 20 zkoušek, je problém znázorněn na obr. 4. Na základě malého počtu zkoušek můžeme určit pouze interval, ve kterém se bude kvantil 5 % základního souboru nacházet. Na obr. 4 je tento interval znázorněn výraznou obousměrnou šipkou, přibližně v rozmezí 47,0 MPa až 53,0 MPa.
Pokud máme splnit požadavek, že charakteristická hodnota bude nižší než kvantil 5 % základního souboru, musíme předpokládat ten nejhorší základní soubor a uvažovat kvantil 5 % na dolní hranici uvedeného intervalu, tj. asi 47,0 Mpa. Jako charakteristickou hodnotu materiálu bychom proto mohli uvažovat nejvýše asi 47,0 MPa.
Z hlediska matematické statistiky jde o jednoznačné řešení, pokud je ještě udaná pravděpodobnost, s jakou mají být příslušné intervaly zjištěny. Tato pravděpodobnost se obvykle nazývá konfidence, aby se odlišila od ostatních pravděpodobností. Konfidence vlastně znamená, jaké procento výsledků, v našem případě odhadů kvantilu 5 %, musí být v uvedeném intervalu. Význam má poměrně vysoká konfidence například 90 %, protože to znamená, že jen v 10 % případů se může stát, že skutečný kvantil 5 % základního souboru je mimo námi určený interval. Statistické tabulky obvykle udávají konfidenci 90 %, 95 % a 99 %.
Tyto dolní hodnoty intervalového odhadu kvantilů jsou uvedeny v tabulkách například v ČSN 01 0250 Statistické metody v průmyslové praxi nebo ISO 12491 Statistical methods for quality control materials and components. Tyto hranice inervalových odhadů se obvykle nazývají toleranční meze.
Z hlediska matematické statistiky jde o naprosto transparentní metodu pro stanovení charakteristické hodnoty, která plně odpovídá definici uvedené v normách. Většina stavebních norem v oblasti požadavků na materiál se omezí na definici v názvosloví a pak stanoví naprosto jiná kritéria, která většinou vůbec nesplňují to, co se uvádí v deklaraci charakteristické hodnoty. Je ovšem zarážející, že tento očividný prohřešek se autoři normy nesnaží ani vysvětlit, ani maskovat.

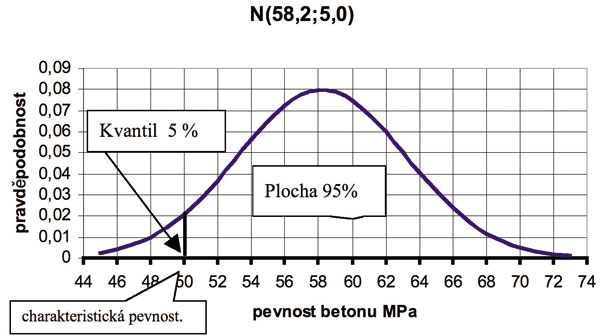
¤ Kvantil 5 % pro zakladni soubor

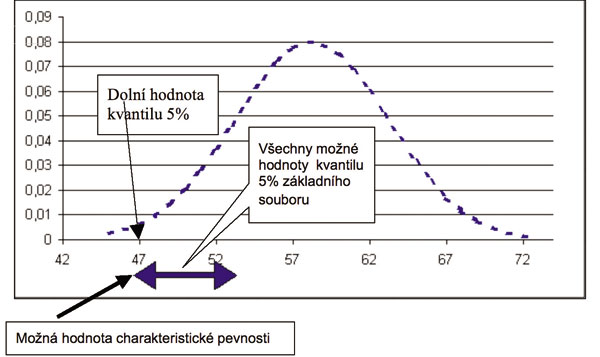
¤ Obr. 4. Intervalovy odhad kvantilu při vyběrovem šetřeni

Jak danou problematiku řeší jednotlivé normy
Pro hodnocení zkoušek betonu platí ČSN EN 206-1. Beton - Část 1: Specifikace vlastnosti, výroba a shoda. Rozeznává kritérium shody pro počáteční výrobu a kritérium shody pro průběžnou výrobu. Při počáteční výrobě musí být průměr z výsledku tří krychlí vetší o 4,0 MPa než charakteristická hodnota (numericky shodná s prvým číslem pevnostní třídy). Takže výběrový průměr ze tří prvků srovnáváme s určitou konstantou. Velikost rozptylu se neuplatní. Při průběžné výrobě se z 35 výsledků určí výběrová směrodatná odchylka a nazve se zcela chybně známá směrodatná odchylka. K této výběrové směrodatné odchylce se určí konfidenční interval. Dále se stanoví výběrový průměr a výběrová směrodatná odchylka z 15 výsledků zkoušek a pokud je směrodatná odchylka ve výše určeném intervalu, může se pracovat se známou směrodatnou odchylkou. Zjištěný průměr z 15 výsledků musí být větší než pevnostní třída a známá směrodatná odchylka vynásobená číslem 1,47. Obdobné kritérium jako dříve, pouze méně přehledné. Tato kritéria zdaleka nezaručují to, co udává deklarace charakteristické hodnoty, že pod charakteristickou hodnotu bude nejvýše 5 % možných výsledků zkoušek. Podrobnějším rozborem lze ukázat, že pod požadovanou charakteristickou hodnotou může být až 40 % výsledků zkoušek.
Pro hodnocení zkoušek betonářské výztuže platí ČSN EN 10080 Ocel pro výztuž do betonu, Svařitelná betonářská ocel - Všeobecně. Pro hodnocení dlouhodobé úrovně jakosti je uvedeno, že aritmetický průměr minus k-násobek směrodatné odchylky musí být větší než specifikovaná charakteristická hodnota. Význam termínu ?specifikovaná charakteristická hodnota? není uveden. Součinitele k odpovídají koeficientům pro jednostranné toleranční meze uvedené v ČSN 01 0250, z hlediska statistiky se jedná o správné hodnoty. Postup, jak se má provádět běžná kontrola například při auditech, není v normě uveden.
Požadavky na zdicí prvky jsou v normách ČSN EN 771-1 Specifikace zdicích prvků - Část 1: Pálené zdicí prvky až ČSN EN 771-6 - Část 6: Zdicí prvky z přírodního kamene. Statistické pojmy jsou v těchto normách zcela zmatené a ustanovení norem jsou často protichůdná. Většina těchto norem udává jako deklarovanou hodnotu průměr výsledků zkoušek, požaduje však, aby výrobce deklaroval, že vyšší hodnotu bude mít 95 % dodávek. Tyto normy se přímo neopoužívají pro navrhování zděných konstrukcí. Z hlediska navrhování zděných konstrukcí uvádí Eurokód 6, obsažený v ČSN EN1996-1-1, empirický vztah pro stanovení charakteristické pevnosti zdiva na základě zdicích prvků a průměrné pevnosti malty. Jak tento vztah odpovídá definici charakteristické hodnoty jako statistické veličině není uvedeno. Pro přímé stanovení charakteristické hodnoty zdiva platí norma ČSN EN 1052-1 Zkušební metody pro zdivo - Část 1: Stanovení pevnosti v tlaku, která udává způsob stanovení charakteristické pevnosti zdiva na základě zkoušek. Při počtu zkoušek méně než 5 udává norma dva empirické vztahy, pro počet zkoušek pět a více doporučuje norma statistické hodnocení, které blíže nespecifikuje. Zkoušek zdiva se provádí málo, takže není dostatek zkušeností s použitím této normy.
Výpočet kvantilu 5 % pro dřevěné konstrukce uvádí ČSN EN 14358 Dřevěné konstrukce výpočet 5% kvantilu charakteristických hodnot a kritéria přijatelnosti pro výběr. Tato norma předpokládá log - normální rozdělení a konfidence 0,75. Předpoklad log - normálního rozdělení není ovšem požadováno ověřit a konfidence 0,75 znamená, že 25 % tj. celá čtvrtina výroby nemusí mít požadovanou vlastnost.

Závěr
Definice a stanovení charakteristických hodnot materiálů se v jednotlivých normách liší a také kritéria pro ověření charakteristické hodnoty jsou v jednotlivých normách výrazně odlišná. Tato kritéria v mnoha případech nezaručují to, co norma deklaruje, že pod charakteristickou hodnotou je nejvýše 5 % možných výsledků zkoušek. Důvodů bude několik. Nedostatečná nebo vůbec žádná koordinace těchto norem, nedostatečné znalosti aplikace statistických metod a v neposlední řadě pravděpodobné ovlivnění tvůrců norem lobbistickými tlaky. Pro projektanta je rozhodující údaj o materiálu v návrhové normě a jeho ověření ho více méně nezajímá. Výrobce materiálu má prioritu materiál prodat a ověření kvality materiálu je nepříjemná povinnost. Inspekční a certifikační orgány, které provádějí kontrolu výrobků mohou vycházet pouze z ustanovení platné normy pro daný výrobek a k výrobcům musejí být vstřícní, protože v opačném případě přejde výrobce v tržním prostředí k jiné dohlížející organizaci.

Použitá literatura
[1] Hatle, J., Likeš, J.: Základy počtu pravděpodobnosti a matematické statistiky. Praha SNTL/ALFA 1974
[2] Laga, J., Likeš, J.:Základní statistické tabulky, Praha 1978, SNTL - Nakladatelství technické literatury
[3] ČSN 01 0250 Statistické metody v průmyslové praxi